Elipsoida adalah bentuk tiga dimensi dari bangun datar elips. Secara umum persamaan elipsoida pada dimensi tiga adalah sebagai berikut:
\[\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} + \frac{{{z^2}}}{{{c^2}}} = 1\]
dimana:
$a$, $b$, dan $c$ adalah sumbu-sumbu pada elipsoida.
Dengan melihat nilai dari $a$, $b$, dan $c$, bangun ruang elipsoida terdiri dari 4 jenis yang berbeda yaitu :
1. Elipsoida triaksial, jika $a > b > c$.
2. Elipsoida oblat, jika $a = b > c$.
3. Elipsoida prolat, jika $a = b < c$.
4. Bola, jika $a = b = c$.
Dari pembagian jenis di atas kita tahu bahwa ternyata bola merupakan bagian dari elipsoida.
Menentukan Rumus volume elipsoida triaksial
Pada elipsoida triaksial berlaku $a > b > c$, sehingga ketiga sumbu pada elipsoida triaksial berbeda panjangnya.
Untuk menentukan rumus volume elipsoida triaksial terlebih dahulu harus mengubah persamaanya dalam $z$ atau dalam bentuk $f(x,y)$.
$\begin{array}{l}
\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} + \frac{{{z^2}}}{{{c^2}}} = 1 \\
\Leftrightarrow \frac{{{z^2}}}{{{c^2}}} = 1 - \frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} \\
\Leftrightarrow {z^2} = {c^2}\left( {1 - \frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}}} \right) \\
\Leftrightarrow z = \pm \sqrt {{c^2}\left( {1 - \frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}}} \right)} \\
\Leftrightarrow z = \sqrt {{c^2}\left( {1 - \frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}}} \right)} \vee z = - \sqrt {{c^2}\left( {1 - \frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}}} \right)} \\
\end{array}$
Menentukan Batas Pengintegralan
Sebelum menentukan batas pengintegralan, terlebih dahulu kita bisa lihat gambar dari elipsoida triaksial pada bidang kartesius.
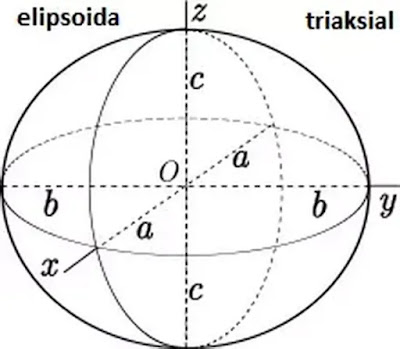
Pada gambar tersebut, titik $O(0,0,0)$ adalah pusat elipsoida. Untuk menghitung volume elipsoida di atas kita tidak harus menghitung keseluruhan. Kita bisa menghitung volume salah satu oktan saja kemudian tinggal kita kalikan $8$, sehingga kita peroleh batas-batas pengintegralan sebagai berikut.
Batas pengintegral untuk $x$ adalah $0$ dan $a$.
Batas pengintegral untuk $y$ adalah $0$ dan untuk batas atas dicari dengan cara berikut:
$\begin{array}{l}
\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1 \\
\Leftrightarrow \frac{{{y^2}}}{{{b^2}}} = 1 - \frac{{{x^2}}}{{{a^2}}} \\
\Leftrightarrow {y^2} = {b^2}\left( {1 - \frac{{{x^2}}}{{{a^2}}}} \right) \\
\Leftrightarrow y = \pm \sqrt {{b^2}\left( {1 - \frac{{{x^2}}}{{{a^2}}}} \right)} \\
\Leftrightarrow y = \sqrt {{b^2}\left( {1 - \frac{{{x^2}}}{{{a^2}}}} \right)} \vee y = - \sqrt {{b^2}\left( {1 - \frac{{{x^2}}}{{{a^2}}}} \right)} \\
\end{array}$
Rumus Volume Elipsoida triaksial
Sama seperti penjelasan di atas, karena kita hanya menghitung volume $1$ oktan saja, maka untuk volume keseluruhan harus dikalikan dengan $8$.
$\begin{array}{l}
V = 8\int\limits_0^a {\int\limits_0^{\sqrt {{b^2}\left( {1 - \frac{{{x^2}}}{{{a^2}}}} \right)} } {zdydx} } \\
V = 8\int\limits_0^a {\int\limits_0^{\sqrt {{b^2}\left( {1 - \frac{{{x^2}}}{{{a^2}}}} \right)} } {\sqrt {{c^2}\left( {1 - \frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}}} \right)} dydx} } \\
V = 8c\int\limits_0^a {\int\limits_0^{b\sqrt {\left( {1 - \frac{{{x^2}}}{{{a^2}}}} \right)} } {\sqrt {\left( {1 - \frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}}} \right)} dydx} } \\
\end{array}$
Misalkan:
$\begin{array}{l}
b\sqrt {\left( {1 - \frac{{{x^2}}}{{{a^2}}}} \right)} = q \\
\Leftrightarrow \sqrt {\left( {1 - \frac{{{x^2}}}{{{a^2}}}} \right)} = \frac{q}{b} \\
\Leftrightarrow 1 - \frac{{{x^2}}}{{{a^2}}} = \frac{{{q^2}}}{{{b^2}}} \\
\end{array}$
Diperoleh:
$\begin{array}{l}
V = 8c\int\limits_0^a {\int\limits_0^q {\sqrt {\left( {\frac{{{q^2}}}{{{b^2}}} - \frac{{{y^2}}}{{{b^2}}}} \right)} dydx} } \\
\end{array}$
$\begin{array}{l}
V = 8\frac{c}{b}\int\limits_0^a {\int\limits_0^q {\sqrt {{q^2} - {y^2}} dydx} } \\
V = 8\frac{c}{b}\int\limits_0^a {\left[ {\frac{1}{2}y\sqrt {{q^2} - {y^2}} + \frac{1}{2}{q^2}{{\sin }^{ - 1}}\left( {\frac{y}{q}} \right)} \right]_0^qdx} \\
V = 4\frac{c}{b}\int\limits_0^a {\left[ {y\sqrt {{q^2} - {y^2}} + {q^2}{{\sin }^{ - 1}}\left( {\frac{y}{q}} \right)} \right]_0^qdx} \\
V = 4\frac{c}{b}\int\limits_0^a {\left[ {\left( {q\sqrt {{q^2} - {q^2}} + {q^2}{{\sin }^{ - 1}}\left( {\frac{q}{q}} \right)} \right) - \left( {0\sqrt {{q^2} - {0^2}} + {q^2}{{\sin }^{ - 1}}\left( {\frac{0}{q}} \right)} \right)} \right]} dx \\
V = 4\frac{c}{b}\int\limits_0^a {\left[ {\left( {0 + {q^2}{{\sin }^{ - 1}}\left( 1 \right)} \right) - \left( {0 + {q^2}{{\sin }^{ - 1}}\left( 0 \right)} \right)} \right]} dx \\
V = 4\frac{c}{b}\int\limits_0^a {\left[ {\left( {{q^2}.\frac{\pi }{2}} \right) - \left( {{q^2}.0} \right)} \right]} dx \\
V = 4\frac{c}{b}\int\limits_0^a {\left( {\frac{\pi }{2}{q^2}} \right)} dx \\
V = 2\pi \frac{c}{b}\int\limits_0^a {{q^2}} dx \\
\end{array}$
Dari sini kembalikan q2 dalam variabel $x$ kembali
$\begin{array}{l}
b\sqrt {\left( {1 - \frac{{{x^2}}}{{{a^2}}}} \right)} = q \Rightarrow {q^2} = {b^2}\left( {1 - \frac{{{x^2}}}{{{a^2}}}} \right) \\
V = 2\pi \frac{c}{b}\left( {a{b^2}\left( {1 - \frac{{{x^2}}}{{{a^2}}}} \right)} \right) \\
\end{array}$
Diperoleh:
$\begin{array}{l}
V = 2\pi \frac{c}{b}\int\limits_0^a {{b^2}\left( {1 - \frac{{{x^2}}}{{{a^2}}}} \right)} dx \\
V = 2\pi bc\int\limits_0^a {\left( {1 - \frac{{{x^2}}}{{{a^2}}}} \right)} dx \\
V = 2\pi bc\left[ {x - \frac{{{x^3}}}{{3{a^2}}}} \right]_0^a \\
V = 2\pi bc\left[ {\left( {a - \frac{{{a^3}}}{{3{a^2}}}} \right) - \left( {0 - \frac{{{0^3}}}{{3{a^2}}}} \right)} \right] \\
V = 2\pi bc\left[ {\left( {a - \frac{a}{3}} \right) - \left( 0 \right)} \right] \\
V = 2\pi bc\left[ {\frac{2}{3}a} \right] \\
V = \frac{4}{3}\pi abc \\
\end{array}$
Kesimpulan
Dari pembuktian dan perhitungan di atas dapat disimpulkan.Volume elipsoida triaksial dengan panjang sumbu masing-masing a, b, dan c adalah
\[\boxed{V = \frac{4}{3}\pi abc}\]
Contoh Soal:
Tentukan volume elipsoida yang memiliki panjang sumbu berturut-turut $2$
cm, $3$ cm, dan $4$ cm.
Jawab:
$\begin{array}{l}
V = \frac{4}{3}\pi abc \\
V = \frac{4}{3}\pi .2.3.4 \\
V = \begin{array}{*{20}{c}}
{32\pi } & {c{m^2}} \\
\end{array} \\
\end{array}$
Demikian semoga bermanfaat

nurhamim86
A Mathematics Teacher who also likes the IT world.


Post a Comment for "Menentukan Rumus Volume Elipsoida Triaksial dengan Menggunakan Integral Ganda"
Mohon untuk memberikan komentar yang baik dan membangun