Kekongruenan pada Bangun Datar
Pengertian Kekongruenan
Dua bangun dikatakan kongruen jika kedua bangun tersebut memiliki bentuk dan ukuran yang sama. Kekongruenan secara umum bisa diterapkan pada bangun datar maupun bangun ruang.
Contoh Bangun yang Kongruen
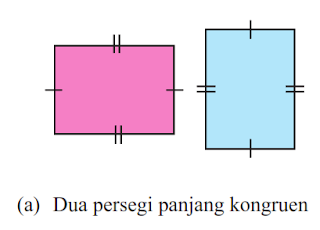
Berikut ini beberapa contoh bangun yang kongruen.
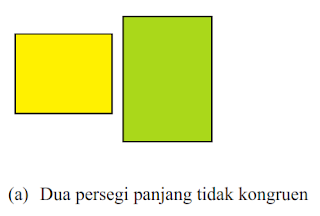
Berikut ini beberapa contoh bangun yang tidak kongruen.
Syarat Dua Bangun Datar yang Kongruen
Dua bangun dikatakan kongruen jika memenuhi dua syarat sebagai berikut:
- Sisi-sisi yang bersesuaian sama panjang.
- Sudut-sudut yang bersesuaian sama besar.
Contoh Soal
Contoh 1
Dari gambar berikut, apakah kedua persegi kongruen? Buktikan!
Jawab
Untuk membuktikan kedua persegi kongruen atau tidak, kita gunakan dua syarat yaitu:
- Sisi-sisi yang bersesuaian sama panjang.
- Sudut-sudut yang bersesuaian sama besar.
- Sisi-sisi yang bersesuaian sama panjang.
- Sudut-sudut yang bersesuaian sama besar.
Panjang sisi persegi (a) adalah $8$.
Panjang sisi persegi (b) adalah $9$.
Dari gambar dapat dibuktikan bahwa sisi-sisi yang bersesuaian tidak sama panjang.
Persegi (a) dan persegi (b) memiliki besar sudut yang sama yaitu ${90^ \circ }$. Jadi sudut yang bersesuaian sama besar.
Dari pembuktian di atas maka disimpulkan kedua persegi tidak kongruen.
Contoh 2
Diketahui trapesium ABCD dan trapesium FEHG adalah kongruen. Jika panjang sisi AD = 12 cm, DC = 13 cm dan EF = 22 cm maka tentukan panjang EH.
Jawab
Diketahui trapesium ABCD dan trapesium FEHG adalah kongruen, maka berlaku:
- Sisi-sisi yang bersesuaian sama panjang.
- Sudut-sudut yang bersesuaian sama besar.
Untuk menentukan panjang EH, kita harus tentukan terlebih dahulu sisi-sisi yang bersesuaian yaitu:
- $AB$ dengan $EF$ sehingga $AB=EF$.
- $BC$ dengan $EH$ sehingga $BC=EH$.
- $CD$ dengan $GH$ sehingga $CD=GH$.
- $AD$ dengan $FG$ sehingga $AD=FG$.
Dengan demikian, karena $AB=EF$ dan $EF=22cm$ maka $AB=22cm$. Untuk menentukan panjang EH kita harus menentukan terlebih dahulu panjang BC.
Untuk menentukan panjang BC bisa menggunakan Teorema Pythagoras, dengan cara sebagai berikut:
Perhatikan segitiga siku-siku $BCC'$ di atas. Panjang $CC'=12cm$, $BC'=22-13=9cm$, panjang BC dapat dicari sebagai berikut:
Karena panjang $BC=15cm$, dan $BC=EH$, maka panjang $EH=15cm$.










Paham pak
ReplyDelete#irmayanti9D