Definite Integrals to Calculate Area

The Area Bounded by a Curve on the X-Axis

The area bounded by the curve $y = f\left( x \right)$ axis $X$, line $x = a$, and line $x = b$ is determined by:

• $L = \int\limits_a^b {f\left( x \right)} dx,\text{for }f\left( x \right) \ge 0$
• $L = - \int\limits_a^b {f\left( x \right)} dx,\text{for }f\left( x \right) \le 0$

The Area Bounded by Multiple Curves

The area bounded by the curve $y = f\left( x \right)$, $y = g\left( x \right)$, the line $x = a$, and $x = b$ is determined by formula:

\[L = \int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]} dx\]

Note that $f\left( x \right) \ge g\left( x \right)$ in closed intervals $a \le x \le b$.

Examples

Calculate the area bounded by the following curves using certain integrals

1. The area bounded by the curve $y=2x$, the $X$ axis, the line $x=1$, and $x=3$.
2. The area bounded by the curve $y = {x^2} + 2$, the axis $X$, the line $x=-1$, and $x=2$.
3. The area bounded by the curve $y = - x$ and $y = {x^2} + 2x$.
4. The area bounded by the curve $y = {x^2}$ and $y = {x^3}$.

Answer

1. The area bounded by the curve $y=2x$, the $X$ axis, the line $x=1$, and $x=3$.

Take a look at the following graph:



From the graph above, at the interval $1 \le x \le 3$ the graph of the function $y=2x$ is above the $X$ axis. The area can be calculated as follows:

$\begin{array}{l} L &= \int\limits_1^3 {f\left( x \right)} dx\\ &= \int\limits_1^3 {2x} dx\\ &= \left[ {{x^2}} \right]_1^3\\ &= \left( {{3^2}} \right) - \left( {{1^2}} \right)\\ &= 9 - 1\\ &= 8 \end{array}$

So, the area bounded by the curve $y=2x$, $X$ axis, line $x=1$, and $x=3$ is $8$ unit area.

2. The area bounded by the curve $y = {x^2} + 2$, the axis $X$, the line $x=-1$, and $x=2$.

Take a look at the following graph:



From the graph above, at the interval $-1 \le x \le 2$ the graph of the function $y = {x^2} + 2$ is above the $X$ axis. The area can be calculated as follows:

$\begin{array}{l} L &= \int\limits_{ - 1}^2 {f\left( x \right)} dx\\ &= \int\limits_{ - 1}^2 {\left( {{x^2} + 2} \right)} dx\\ &= \left[ {\frac{1}{3}{x^3} + 2x} \right]_{ - 1}^2\\ &= \left( {\frac{1}{3}{2^3} + 2.2} \right) - \left( {\frac{1}{3}{{\left( { - 1} \right)}^3} + 2.\left( { - 1} \right)} \right)\\ &= \left( {\frac{8}{3} + 4} \right) - \left( { - \frac{1}{3} - 2} \right)\\ &= \frac{8}{3} + 4 + \frac{1}{3} + 2\\ &= 9 \end{array}$

So, the area bounded by the curve $y = {x^2} + 2$, axis $X$, line $x=-1$, and $x=2$ is $9$ unit area.

3. The area bounded by the curve $y = - x$ and $y = {x^2} + 2x$.

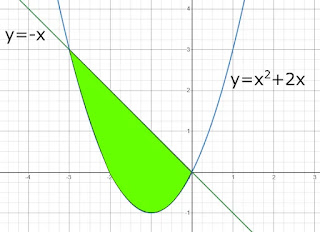
Take a look at the following graph:



From the graph above, suppose $f\left( x \right) = y = - x$ and $g\left( x \right) = y = {x^2} + 2x$ then $f\left( x \right) \ge g\left( x \right)$ in the shaded area. To determine the upper and lower limits of the integration can be searched in the following way:

$\begin{array}{l} f\left( x \right) &= g\left( x \right)\\ \Leftrightarrow - x &= {x^2} + 2x\\ \Leftrightarrow {x^2} + 2x &= - x\\ \Leftrightarrow {x^2} + 2x + x &= 0\\ \Leftrightarrow {x^2} + 3x &= 0\\ \Leftrightarrow x\left( {x + 3} \right) &= 0\\ x = 0 \vee x + 3 = 0\\ x = 0 \vee x = - 3 \end{array}$

We get the lower limit of $x = - 3$ and the upper limit of $x = 0$. The area can be calculated as follows:

$\begin{array}{l} L &= \int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]} dx\\ &= \int\limits_{ - 3}^0 {\left[ {\left( { - x} \right) - \left( {{x^2} + 2x} \right)} \right]} dx\\ &= \int\limits_{ - 3}^0 {\left[ { - x - {x^2} - 3x} \right]} dx\\ &= \int\limits_{ - 3}^0 {\left[ { - {x^2} - 4x} \right]} dx\\ &= \left[ { - \frac{1}{3}{x^3} - 2{x^2}} \right]_{ - 3}^0\\ &= \left( { - \frac{1}{3}{{.0}^3} - {{2.0}^2}} \right) - \left( { - \frac{1}{3}{{\left( { - 3} \right)}^3} - 2{{\left( { - 3} \right)}^2}} \right)\\ &= 0 - \left( { - \frac{1}{3}\left( { - 27} \right) - 2.9} \right)\\ &= 0 - \left( {9 - 18} \right)\\ &= 9 \end{array}$

So, the area bounded by the curve $y = - x$ and $y = {x^2} + 2x$ is $9$ unit area.

4. The area bounded by the curve $y = {x^2}$ and $y = {x^3}$.

Take a look at the following graph:



From the graph above, suppose $f\left( x \right) = y = {x^2}$ and $g\left( x \right) = y = {x^3}$ then $f\left ( x \right) \ge g\left( x \right)$ in the shaded area. To determine the upper and lower limits of the integration can be searched in the following way:

$\begin{array}{l} f\left( x \right) &= g\left( x \right)\\ \Leftrightarrow {x^2} &= {x^3}\\ \Leftrightarrow {x^2} - {x^3} &= 0\\ \Leftrightarrow {x^2}\left( {1 - x} \right) &= 0\\ \Leftrightarrow {x^2} = 0 \vee 1 - x = 0\\ \Leftrightarrow x = 0 \vee x = 1 \end{array}$

We get the lower limit of $x = 0$ and the upper limit of $x = 1$. The area can be calculated as follows:

$\begin{array}{l} L &= \int\limits_0^1 {\left[ {f\left( x \right) - g\left( x \right)} \right]} dx\\ &= \int\limits_0^1 {\left[ {{x^2} - {x^3}} \right]} dx\\ &= \left[ {\frac{1}{3}{x^3} - \frac{1}{4}{x^4}} \right]_0^1\\ &= \left( {\frac{1}{3}{{.1}^3} - \frac{1}{4}{{.1}^4}} \right) - \left( {\frac{1}{3}{{.0}^3} - \frac{1}{4}{{.0}^4}} \right)\\ &= \left( {\frac{1}{3} - \frac{1}{4}} \right) - 0\\ &= \frac{1}{{12}} \end{array}$

So, the area bounded by the curves $y = {x^2}$ and $y = {x^3}$ is $\frac{1}{{12}}$ unit area.